Cut-off wavelength of single-mode and polarization-maintaining fibers

Cut-off wavelength of single-mode or PM fibers

Cut-off wavelength

The cut-off wavelength λ_co is defined as the shortest wavelength for which the fiber is single-mode. The mode field can only have a Gaussian intensity distribution and rotational symmetry at wavelengths above λ_co.

If the wavelength of the guided radiation is shorter than the cut-off wavelength, two or more modes are guided. The beam and intensity profile then differ significantly from a Gaussian distribution. The mode field distribution depends on bending or temperature variations (butterfly effect).

The wavelength range which the fiber can operate (operation range) depends on the fiber . outside the operating range, even a slight bending of the fiber (as well as micro-bends) result in attenuation of the guided radiation (increased bending loss).

When more than one fiber can be used for a particular wavelength, the fiber with a cut-off wavelength closer to the operation wavelength should be chosen.

The measured cut-off wavelength λ_co of a fiber may be 10% less than the nominal value because of manufacturing tolerances. Carefully selected fibers with characterized values are available on request.

Mode field of a singlemode fiber used within the operation range

Gaussian mode field within a step index single-mode. The transmitted wavelength lies within the opertaion range of the fiber.

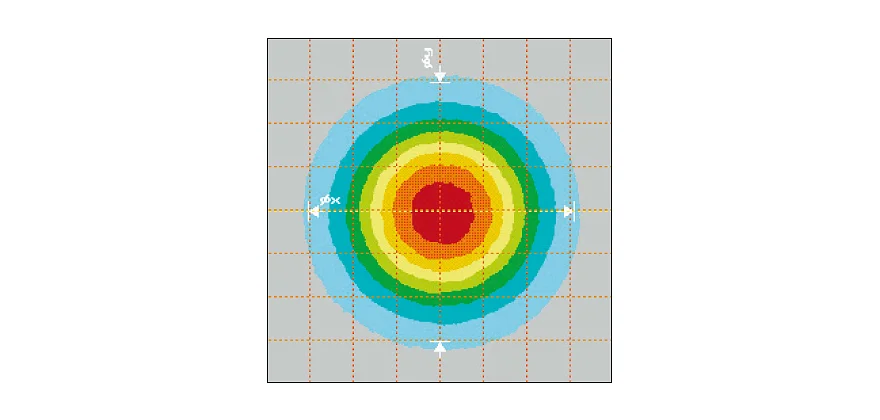
Gaussian mode field of a single-mode fiber

Resulting intensity distribution at fiber exit

The resulting intensity distribution at the fiber exit is Gaussian.

Mode field of a singlemode fiber used below cut-off

For a transmitted wavelength below cut-off the mode field within the step index fiber shows multiple modes (butterfly effect).

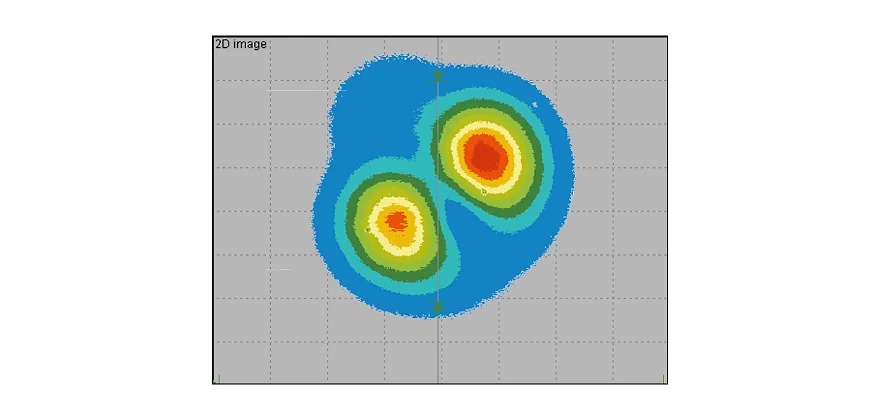
Resulting Butterfly effect

The resulting intensity profile at the fiber exit is also non-Gaussian.